2.11 Alternate Symbols

Symbols like ÷, √, ∫ and ⅆ are available on Myron's specialized Android keyboard (see §1.6) and the desktop keyboard aide (see §1.6.2). When entering expressions directly using a standard keyboard, special symbols can also be created by typing a $ character or a ` character (the so-called tick character) followed by a single standard character to produce special symbols and Greek letters. Such two-character sequences are called $ escapes and tick escapes. Escaped characters are translated into their Unicode equivalents by the parser.

2.11.1 Tick Escapes

The association between Roman letters and Greek letters used by the tick-escape mechanism is shown in Figure 2.55. The table contains some peculiarities due to the lack of a one-to-one mapping between Roman and Greek alphabets.

The Greek alphabet contains only 24 characters, so `q and `w simply map to spaces.
eta should come before theta, but the character eta maps naturally to H, while G, having no Greek counterpart but being very close to H, is used for theta.
xi, coming between nu and omicron, has no Roman counterpart, so it is assigned to J, which has no Greek counterpart.

Roman	Greek	Roman	Greek	Name
a	α	A	Α	alpha
b	β	B	Β	beta
c	γ	C	Γ	gamma
d	δ	D	Δ	delta
e	ε	E	Ε	epsilon
f	ζ	F	Ζ	zeta
g	θ	G	Θ	theta
h	η	H	Η	eta
i	ι	I	Ι	iota
j	ξ	J	Ξ	xi
k	κ	K	Κ	kappa
l	λ	L	Λ	lambda
m	μ	M	Μ	mu
n	ν	N	Ν	nu
o	ο	O	Ο	omicron
p	π	P	Π	pi
q		Q
r	ρ	R	Ρ	rho
s	σ	S	Σ	sigma
t	τ	T	Τ	tau
u	υ	U	Υ	upsilon
v	φ	V	Φ	phi
w		W
x	χ	X	Χ	chi
y	ψ	Y	Ψ	psi
z	ω	Z	Ω	omega

Figure 2.55 Tick mapping

2.11.2 $ Escapes

The characters used in $ escapes have been chosen to be mnemonic, although some of the choices have become quite creative in order to handle collisions. For example, $s is the symbol √ and $S is the symbol for summation, ∑.

Figure 2.56 defines the $ escapes for the special symbols used by Myron.

$a	∧	$A	∠	$b	ɓ	$c	‖
$C	⌈	$d	ⅆ	$D	∂	$e	ⅇ
$E	∃	$f	∀	$F	⌊	$g	∇
$G	≥	$i	∫	$j	ⅉ	$l	λ
$L	≤	$M	∖	$n	∈	$N	≠
$o	∨	$p	ℼ	$P	∏	$r	ɽ
$s	√	$S	∑	$t	ʈ	$u	∪
$v	ʋ	$x	⊕	$X	𝕏	$Y	𝕐
$!	ɪ	$*	×	$+	±	$-	→
$.	°	$/	÷	$0	⊥	$1	⊤
$8	∞	$<	<	$=	⇒	$>	>
$^	∩	${	«	$\|	¦	$}	»
$~	¬

Figure 2.56 $ Escapes

2.11.3 Alternate Representations

The desktop environment provides an opportunity to interoperate with other mathematics and text editing programs. Additional controls to the right of the text input and output areas in the desktop version of Myron support interoperability.

2.11.3.1 Translate to $ and ` escapes

Sometimes a Myron expression has to be translated from special-symbol form to escaped form. For example, the source text of this guide is created using a standard text editor. The book's markup uses embedded escaped expressions that are parsed and rendered into displayable forms. The escaped expressions are obtained from Myron expressions by harvesting the contents of the text-output area (using Ctrl-a Ctrl-c ) after touching the button. The button encodes special symbols of the expression in the output area using escaped characters.

can also be used to learn the escaped form for commonly used symbols.

2.11.3.2 Translate to TEX

Myron expressions can also be translated into the notation used by Tex by touching the button. Like escaped expressions, Tex-formatted expressions can be harvested from the text-output area.

2.11.3.3 Math Input Control

Since Windows 7, the Math Input Control (MIC) has been available to recognize hand-written mathematical expressions. In the Windows version of Myron (both desktop and tablet), the MIC control displays the MIC window. When the Insert button in the MIC window is touched, the entered expression will be converted to a Myron expression and displayed in the algebra workspace. An example is shown in Figure 2.57.

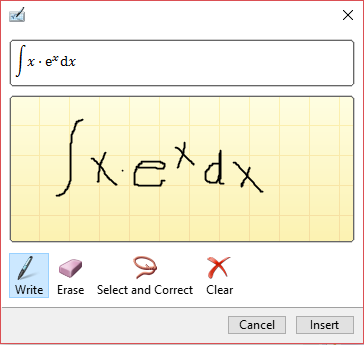
The Math Input Control has its own notion of what constitutes a correct mathematical expression. This means that not all expressions considered valid in the MIC window can be translated into valid Myron expressions. Still, MIC provides a way to enter portions of complex expressions that can be manipulated into larger expressions in Myron.

2.11.3.4 OpenMath

MIC communicates with Myron using an XML-based markup language called MathML. Like , MathML does not describe content, just presentation. However, there is a mechanism for encoding semantic information in MathML. The standard for this is OpenMath, maintained by the OpenMath Society. MathML used in this way is sometimes referred to as Content MathML.

Myron can both parse and render Content MathML (CMML). The MML control near the Text Output area opens a new window and displays the active expression rendered to Content Mathml. Touching the Insert button at the bottom of the CMML I/O window parses the XML into a Myron expression, replacing the active expression in the algebra workspace.

Using Copy , the XML in the CMML I/O window can be transferred to other applications via the system clipboard. Using Replace , XML can be imported from other sources, again via the clipboard. After pasting XML into the window, the Preview button translates the XML into an expression in Myron syntax and displays it in the lower window. Insert performs the same translation but transfers the result to the algebra workspace instead of displaying it in the lower window. If any errors occur during the translation, they are also displayed in the lower window.